OGC 标准介绍 WKT

# WKT 描述的几何对象

WKT（Well-known Text）可以通过文本来描述几何对象。下面的例子可以比较快速、直观地说明什么是 WKT：

几何类型	WKT 例子	说明
Point	Point (10 10)	点
LineString	LineString ( 10 10, 20 20, 30 40)	有 3 个节点的线
Polygon	Polygon ((10 10, 10 20, 20 20, 20 15, 10 10))	只有 1 个外环的多边形
MultiPoint	MultiPoint((10 10),(20 20))	多点
MultiLineString	MultiLineString((10 10, 20 20),(15 15, 30 15))	多线
MultiPolygon	MultiPolygon(((10 10, 10 20, 20 20, 20 15, 10 10)),((60 60, 70 70, 80 60, 60 60 )))	多面
GeometryCollection	GeometryCollection(POINT (10 10),POINT (30 30),LINESTRING (15 15, 20 20))	几何集合
PolyhedralSurface	PolyhedralSurface Z(((0 0 0, 0 0 1, 0 1 1, 0 1 0, 0 0 0)),((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)),((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)),((1 1 0, 1 1 1, 1 0 1, 1 0 0, 1 1 0)),((0 1 0, 0 1 1, 1 1 1, 1 1 0, 0 1 0)),((0 0 1, 1 0 1, 1 1 1, 0 1 1. 0 0 1)))	多个表面构成的立方体
Tin	Tin Z(((0 0 0, 0 0 1, 0 1 0, 0 0 0)),((0 0 0, 0 1 0, 1 0 0, 0 0 0)),((0 0 0, 1 0 0, 0 0 1, 0 0 0)),((1 0 0, 0 1 0, 0 0 1, 1 0 0)))	4 个三角形构成的 TIN 网格
Point	Point Z (10 10 5)	三维点
Point	Point ZM (10 10 5 40)	带 M 值的三维点
Point	Point M (10 10 40)	带 M 值的二维点

# WKB 描述的几何对象

WKB（Well-known Binary）通过序列化的字节对象来描述几何对象。在 WKB 中主要涉及两种数值类型：一种是 uint32，占 4 个字节，用以存储节点数、几何对象类型等信息；另一种是 double，占 8 个字节，用以存储节点坐标值。其中的几何对象类型对应的整数可以参考下表：

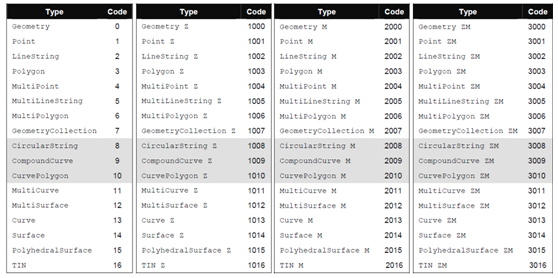
除此之外，WKB 在第一位还存储了一个额外的字节用来标识字节序（0=Big-Indian，1=Little-Indian）。因此，对于一个点（不带 M 值的二维点）来说，它的 WKB 描述应该类似下面的结构，总共占据 21 个字节：

对于有 2 个节点的线来说，WKB 描述应该包含 41 个字节：

对于仅有 1 个外环，由 3 个节点构成的多边形来说，WKB 描述则应该包含 77 个字节：

# WKT 描述的空间参考

WKT 除了可以描述几何对象，也可以描述空间参考。通过 2 个例子可以很直观地看到如何通过文本来描述空间参考。

对于一个地理坐标系，比如最常见的 WGS84 坐标系统，WKT 描述是这样的：

GEOGCS[
	('GCS_WGS_1984',
	DATUM[('D_WGS_1984', SPHEROID[('WGS_1984', 6378137.0, 298.257223563)])],
	PRIMEM[('Greenwich', 0.0)],
	UNIT[('Degree', 0.0174532925199433)],
	AUTHORITY[('EPSG', 4326)])
];

1
2
3
4
5
6
7

“GEOGCS”表明其后紧随的“[ ]”中描述的是一个地理坐标系统。该坐标系统名称为“GCS_WGS_1984”；采用的大地基准面为“D_WGS_1984”，该基准面近似椭球体的长轴为 6378137.0 米、扁率为 298.257223563；以格林威治 0 度经线为起始经线；地图单位为度，该单位的转换因子[2] 为 0. 0174532925199433（π/180）；最后，该坐标系统在 EPSG[3] 中的编码为“4326”。

对于一个投影坐标系，比如 WGS84 Web Mercator（Auxiliary Sphere）坐标系统，WKT 描述是这样的：

PROJCS[
	('WGS_1984_Web_Mercator_Auxiliary_Sphere',
	GEOGCS[
		('GCS_WGS_1984',
		DATUM[('D_WGS_1984', SPHEROID[('WGS_1984', 6378137.0, 298.257223563)])],
		PRIMEM[('Greenwich', 0.0)],
		UNIT[('Degree', 0.0174532925199433)])
	],
	PROJECTION['Mercator_Auxiliary_Sphere'],
	PARAMETER[('False_Easting', 0.0)],
	PARAMETER[('False_Northing', 0.0)],
	PARAMETER[('Central_Meridian', 0.0)],
	PARAMETER[('Standard_Parallel_1', 0.0)],
	PARAMETER[('Auxiliary_Sphere_Type', 0.0)],
	UNIT[('Meter', 1.0)],
	AUTHORITY[('EPSG', 3857)])
];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

类似的，“PROJCS”代表这是一个投影坐标系。投影坐标系中必然会包括一个地理坐标系，这里的地理坐标系就是“GCS_WGS_1984”，这个地理坐标系的定义和上面的类似。下面紧跟着的是投影的相关参数，“Mercator_Auxiliary_Sphere”是采用投影的名称，这个投影坐标系以 0 度经线为中央经线进行投影；坐标系的单位为米（显然，转换因子就为 1.0），而该坐标系的 EPSG 编码为“3857”。

WebGIS

Choose mode